O QUE É NUMERO Pi?

NUMERO PI Na matemática, o número  é uma proporção numérica que tem origem na relação entre o perímetro de umacircunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro  então aquele número é igual a  É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circularou número de Ludolph.

Notação  Os primeiros a utilizarem a letra grega  foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual1 foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.  §Valor de   O valor de  pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar  por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima  por 3,1415926. Para cálculos mais precisos pode-se utilizar  com 52 casas decimais.  Para cálculos ainda mais precisos pode-se obter aproximações de através de algoritmos computacionais. Um engenheiro japonês e um estudante americano de ciências da computação calcularam, usando um computador com doze núcleos físicos, cinco trilhões de dígitos, o equivalente a 6 terabytes de dados.  A aproximação do número pi até a tricentésima casa decimal:  = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273

Aproximações para   Desde a Antiguidade, foram encontradas várias aproximações de  para o cálculo da área do círculo.5 Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a  seria  embora também seja encontrado o valor   Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de .   Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor  já ser conhecido como aproximação

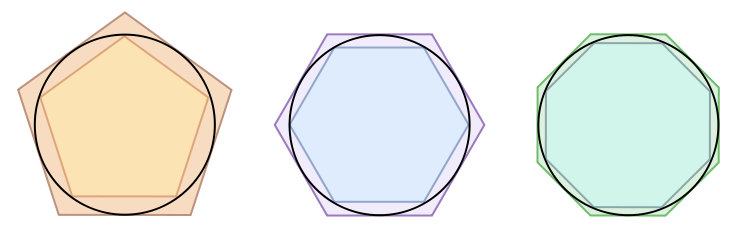
Métodos de cálculo  Existem muitas formas de se obter o valor aproximado de  através de métodos numéricos. Consideramos que [[]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões. §Método clássico para o cálculo de   Método clássico para o cálculo de  A primeira tentativa rigorosa de encontrar  deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.  Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou pi tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes. A "busca" pelo valor de  chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927. Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62.000. O resultado é aproximadamente uma circunferência de diâmetro 20.000". Analisando matematicamente e considerando a equação citada anteriormente de

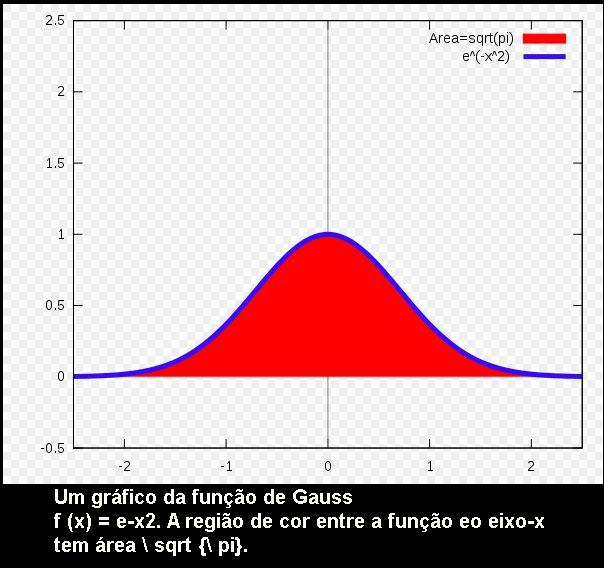
O valor de  portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular. O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Ghiyath al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de  com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de  com as supracitadas 35 casas decimais. Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para  Uma aproximação de  que apresenta diferença de aproximadamente 2,7e-7 é a seguinte: §

Formulação matemática do método de Arquimedes  Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados. Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos: Temos formado um triângulo isósceles, de base l e lados r=1: O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto: Dessa forma, o perímetro do polígono será de: Como  é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos: Aplicando transformações trigonométricas, a fórmula acima pode ser simplificada para:

Métodos estatísticos  Outro método interessante para o cálculo de  pode ser realizado através de Monte Carlo utilizando-se a estatística. Nesse método são sorteados aleatoriamente pontos num quadrado compreendido entre as coordenadas  e  Em seguida calcula-se a distância dos pontos sorteados  até a origem O = (0, 0).  pode ser aproximado através do número de pontos inscritos na circunferência de raio 1 em relação ao total de pontos sorteados no quadrado de lado 1. No exemplo ao lado ,  Outro método que utiliza a estatística de Monte Carlo para o cálculo de  é conhecido como Agulha de Buffon, proposto no século XVIIIpelo naturalista francês Georges de Buffon.

Métodos de séries infinitas  O francês François Viète, estudando o método de Arquimedes, desenvolveu a seguinte série para o cálculo de  em 1593: O matemático John Wallis, desenvolveu outra série infinita em 1655: Outra série conhecida para o cálculo de  foi desenvolvida por Leibniz em 1682, utilizando-se da série de Taylor para a função arctan(x), tomando-se x=1 e, por conseguinte, arctan(1)=/4. Johann Heinrich Lambert publicou, em 1770, uma série na forma de divisões infinitas:

Métodos de cálculo numérico Um dos estudos dos métodos de cálculo numérico é obter a raiz de uma função. Quando consideramos a função  sabemos que  Os principais métodos do calculo numérico para a obtenção da raiz da função  podem incluir uma busca binária no intervalo  onde se sabemos que   e   então podemos aprimorar o intervalo para:  se  e  se  Partindo-se do intervalo  esse método permite refiná-lo sucessivamente para os intervalos e assim sucessivamente. Ainda no cálculo numérico, o método de Newton-Raphson, mais eficiente que uma busca binária permite obter aproximações sucessivas para a raiz da função  utilizando um ponto inicial  exigindo que conheçamos  Tomando-se  e considerando-se que por Newton-Rapson temos a seguinte série para  Um método otimizado de cálculo numérico para o cálculo de  através das raízes de uma função pode ser obtido pela simplificação pois na proximidade de     Notemos que nesses algoritmos de cálculo numérico considera-se  como trancendental, uma vez que a função  não pode ser escrita através de um polinômio finito de coeficientes racionais; a função  é obtida através da expansão da série de Taylor.

Algoritmo de Gauss-Legendre  O Algoritmo de Gauss-Legendre,  que é um método de cálculo numérico de aproximações succesivas, foi utilizado por Yasumasa Kanada para obter o recorde mundial no cálculo de casas decimais de pi em 2002.12 §Método de cálculo isolado das decimais   Em 1995, David Harold Bailey, em colaboração com Peter Borwein e Simon Plouffe, descobriu uma fórmula de cálculo de π, uma soma infinita (frequentemente chamada fórmula BBP): Essa fórmula permite calcular facilmente a enésima decimal binária ou hexadecimal de  sem ter que calcular as decimais precedentes. O sítio de Bailey contém sua derivação e implementação em diversas linguagens de programação. Graças a uma fórmula derivada da fórmula BBP, o 4 000 000 000 000 000° algarismo de  em base 2 foi obtido em 2001. §Grandezas que dependem de   Várias relações matemáticas dependem do conhecimento da constante  as mais conhecidas a nível didático são: Perímetro de uma circunferência:  Área do círculo :  Volume de uma esfera:   também está nas fórmulas gravitacionais e do eletromagnetismo da física.

Irracionalidade e transcendência de     O perímetro da circunferência é 3,1416... vezes maior que o diâmetro, sendo a razão perímetro/diâmetro o (pi) Johann Heinrich Lambert demonstrou em 1761 que se  é racional e diferente de  então nem  nem  podem ser racionais . Como  segue-se que  é irracional, e portanto que  é irracional.     Lindemann provou em 1882 que  é transcendente utilizando o método utilizado por Hermite para provar que e é transcendente. Isto significa que  não pode ser a solução de nenhuma equação algébrica de coeficientes racionais. A transcendência de  estabelece a impossibilidade de se resolver o problema da quadratura do círculo: é impossível construir, somente com régua e um compasso euclideanos, um quadrado cuja área seja rigorosamente igual à área de um determinado círculo. §Questões sem resposta  A questão em aberto mais importante é a de saber se  é um número normal, isto é, se qualquer sucessão de algarismos aparece nas decimais de  como seria de se esperar em uma sequência infinita e completamente aleatória de algarismos. Isso deveria ser verdadeiro em qualquer base, e não somente na base 10. Também não se sabe que algarismos aparecem um número infinito de vezes na constituição de  Bailey e Crandall demonstraram em 2000 que a existência da fórmula Bailey-Borwein-Plouffe mencionada acima e de fórmulas similares implicam a normalidade de  em base 2.

Cronologia do cálculo de   Matemático Ano Casas Decimais Egípcios (Papiro de Rhind) 1650 A.C. 1 Arquimedes 250 A.C. 3 Zu Chongzhi 480 D.C. 7 Ghiyath al-Kashi 1424 16 Ludolph van Ceulen 1596 35 Georg von Vega 1794 126 Gauss 1824 200 William Shanks 1874 527 Levi B. Smith, John W. Wrench 1949 1.120 Daniel Shanks, John W. Wrench 1961 100.265 Jean Guilloud, M. Bouyer 1973 1.000.000 Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura 1982 16.777.206 Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo 1987 134.217.700 Chudnovskys 1989 1.011.196.691 Yasumasa Kanada, Daisuke Takahashi 1997 51.539.600.000 Yasumasa Kanada, Daisuke Takahashi 1999 206.158.430.000 Yasumasa Kanada 2002 1.241.100.000.000 Daisuke Takahashi 2009 2.576.980.370.000 15 Fabrice Bellard 2010 2.699.999.990.000 16 Shigeru Kondo & Alexander Yee 2010/08/02 5.000.000.000.000 17 Shigeru Kondo & Alexander Yee 2011 10.000.000.000.000 18 The Santa Clara University 2013 8.000.000.000.000.000 19